IMPORTANT Sample paper Class 10 Maths 2023 CBSE

Table of Contents

Sample paper Class 10 Maths 2023 CBSE

Class – X (Session: 2022-23)
Subject- Mathematics (Standard)

Time Allowed: 3Hrs Maximum Marks: 80

General Instructions:
This Question Paper has 5 Sections A-E
Section A has 20 MCQs carrying 1mark each
Section B has 5 questions carrying 02 marks each.
Section C has 6 questions carrying 03 marks each.
Section D has 4 questions carrying 05 marks each.
Section E has 3 case based integrated units of assessment (04 marks each) with sub- parts of the values of 1, 1 and 2 marks each respectively.
All Questions are compulsory. However, an internal choice in 1 Question of 5 marks, 1 Question of 3 marks and 1 Question of 2 marks has been provided. An internal choice has been provided in the 2 marks questions of Section E
Draw neat figures wherever required. Take π =22/7 wherever required if not stated.

SECTION A Section A consists of 20 questions of 1mark each

1. A natural number, when increased by 12, equals 160 times its reciprocal. Find the number.
(a) 3 (b) 8 (c) 9 (d) 7
2. The nth term of an A.P. is given by an = 3 + 4n. The common difference is
(a) 7 (b) 3 (c) 4 (d) 1
3. The (n – 1)th term of an A.P. is given by 7,12,17, 22,… is
(a) 5n + 2 (b) 5n + 3 (c) 5n – 5 (d) 5n – 3
4. In ∆ ABC, DE || AB. If CD = 3 cm, EC = 4 cm, BE = 6 cm, then DA is equal to
(a) 7.5 cm (b) 3 cm (c) 4.5 cm (d) 6 cm
5. A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
(a) 25.6 (b) 20.4 (c) 23.7 (d) 32.5
6. The point which divides the line segment joining the points (7, –6) and (3, 4) in ratio 1 : 2 internally lies in the
(a) I quadrant (b) II quadrant (c) III quadrant (d) IV quadrant
7. A line intersects the y-axis and x-axis at the points P and Q, respectively. If (2, –5) is the mid point of PQ, then the coordinates of P and Q are, respectively.
(a) (0, – 5) and (2, 0) (b) (0, 10) and (– 4, 0) (c) (0, 4) and (– 10, 0) (d) (0, – 10) and (4, 0)
8. If A is an acute angle and tanA +cotA =2 then the value of sin3A+cos3A is
(a) 1 (b) 1/2 ( c) √2 (d) √2/2

9. Value of ( sin30° + cos30°) – (sin 60° + cos60°) is
(a) – 1 (b) 0 (c) 1 (d)2
10. In figure AT is a tangent to the circle with centre O such that OT = 4 cm and ∠OTA = 30°. Then AT is equal to

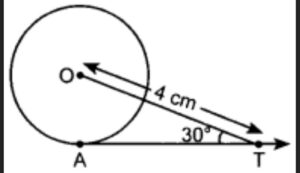
(a) 4 (b) 2 cm. (c) 2√3 cm (d) 4√3 cm
11. The perimeter of the sector with radius 10.5 cm and sector angle 60° is
(a) 32 cm (b) 23 cm (c) 41 cm (d) 11 cm
12. If the perimeter of a semicircular protractor is 72 cm where π = 22/7, then the diameter of protractor is
(a) 14 cm (b) 33 cm (c) 28 cm (d) 42 cm
13. Volumes of two spheres are in the ratio 64:27. The ratio of their surface areas is:
(a)3 : 4 (b)4 : 3 (c) 9 : 16 (d) 16:9
14. If the area of three adjacent faces of cuboid are x, y and z respectively, then the volume of cuboid is:
(a) xyz (b) 3xyz (c) √xyz (d) √3xyz
15. For the following distribution. the sum of lower limits of the modal class and the median class is
(a) 15 (b) 30 (c) 25 (d) 35

16. Three vertices of a parallelogram ABCD are A (1,4) , B(-2,3) , and C(5,8).The
x-coordinate of 4th vertex D is
(a) 8 (b) 9 (c) 7 (d) 6
17. If two different dice are rolled together, the probability of getting an even number on both dice is:
(a) 1/36 (b) 1/2 (c) 1/6 (d) 1/4
18.In a family of 3 children, the probability of having atleast one boy is:
(a) 7/8 (b) 1/8 (c) 5/8 (d) 3/4

DIRECTION: In the question number 19 and 20, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:
(a) Both assertion (A) and reason (R ) are true and reason (R ) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R ) are true but reason (R ) is not the correct explanation of assertion (A).
(c) Assertion (A) is true but reason (R )is false.
(d) Assertion (A) is false but reason (R ) is true.

19. Assertion (A): If ∆ABC and ∆PQR are congruent triangles, then they are also similar triangles.
Reason : (R ) All congruent triangles are similar but all similar triangles need not be congruent.

20. Assertion (A): If the outer and inner diameter of a circular path is 10 m and 6 m respectively, then area of the path is 16π m2.
Reason (R): If R and r be the radius of outer and inner circular path respectively, then area of circular path = 2π(R2 – r2).
SECTION B
Section B consists of 5 questions of 2 marks each.

21. In ∆ABC, DE || BC, find the value of x.

22. If sinA + sin²A = 1 , then find the value of cos²A + cos⁴A.

OR

If x = 2sin²A, y= 2cos²A+1, then find the value of x+y.
23. The tops of two towers of height x and y standing on level ground, subtend angles of 30 degree and 60 degree respectively at the centre of the line joining their feet. Find x:y
24. In fig. ∆ ABC is circumscribing a circle. Find the length of BC.

25. Area of a sector of a circle of radius 14 cm is 154 cm2. Find the length of the corresponding arc of the sector. [Use π = 22/7]
SECTION C
Section C consists of 6 questions of 3 marks each.

26. The sum of the ages of a father and his son is 45 years. 5 years ago, the product of their ages (in years) was 124. Find their present ages.
27. The 17th term of an AP is 5 more than twice its 8th term. If the 11th term of the AP is 43, find its nth term.
28. Prove that SinA/(1+CosA) + (1+CosA)/SinA =2CosecA

OR

Prove that SecA (1-SinA) (SecA+TanA) =1
29. The king, queen and jack of clubs are removed from a deck of 52 playing cards and the remaining cards are shuffled. A card is drawn from the remaining cards. Find the probability of getting a card of (i)Heart (ii) Queen (iii) Clubs
30. From a solid cylinder of height 14 cm and base diameter 7 cm, two equal conical holes each of radius 2.1 cm and height 4 cm are cut off. Find the volume of the remaining solid.
31. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

SECTION D
Section D consists of 4 questions of 5 marks each.

32. The speed of boat in still water is 15 km/h. It can go 30 km upstream and return downstream to the original point in 4 hours and 30 minutes. Find the speed of the stream.
OR
An old lady while boarding a plane got hurt and captain immediately called the medical aid. Then the plane left with the lady 30 minutes later than the scheduled time. In order to reach its destination 1500 km away in time, it has to increase its speed by 250 km per hour from its usual speed. Find the usual speed to the plane.
33. Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides at different points, the other two sides are divided in the same ratio.
34. A vessel is in the form of an inverted cone. Its height is 8 cm and radius of its top, which is open, is 5 cm. It is filled with water upto the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one fourth of the water flows out. Find the number of lead shots dropped in the vessel.
35. The mean of the following frequency table is 57.6. Find the frequencies f1 and f2

SECTION E
Case study based questions are compulsory
36. Your friend Veer wants to participate in a 200 m race. He can currently run that distance in 51 seconds and with each day of practice it takes him 2 seconds less. He wants to do in 31seconds

Sample paper Class 10 Maths 2023 CBSE

Sample paper Class 10 Maths 2023 CBSE

(a) Write the AP for the given situation.
(b) What is the minimum number of days he needs to practice till his goal is achieved ?
( c) If nth term of an AP is given by an= 2n+3 , then find common difference of the AP
OR
The value of x, for which 2x, x + 10, 3x + 2 are 3 consecutive terms of an AP.
37. Amit standing on a horizontal plane, finds a bird flying at a distance of 200 m from him at an elevation of 300 . Sonu standing on the roof of a 50m high building, finds the angle of elevation of the same bird to be 45⁰. Amit and Sonu are on opposite sides of the bird.

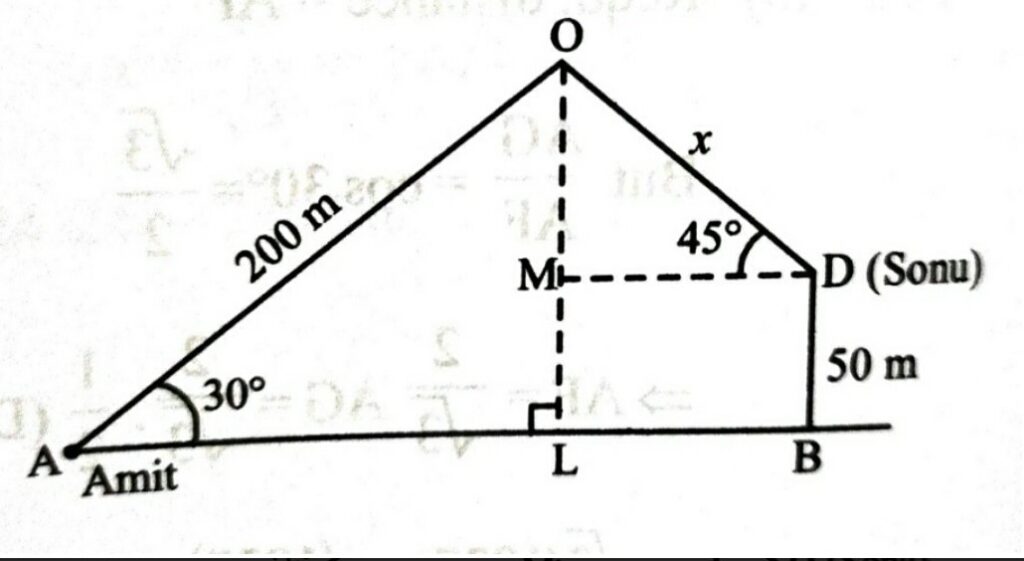
(i) Find the height of the bird from the ground level
(ii) Find the height of the bird from level of Sonu.
(iii) Find the distance of the bird from Sonu.
OR
Find the distance LB.
38 Students of the class X are on the visit of Sansad Bhawan.Teacher assign them the activity to observe and take some pictures to analyses the seating arrangement between various MP and Speaker based on coordinate geometry. The staff tour guide explained various facts related to Math’s of Sansad Bhawan to the students, students were surprised
when teacher ask them to apply coordinate geometry on the seating arrangement`of MP’s and speakers.

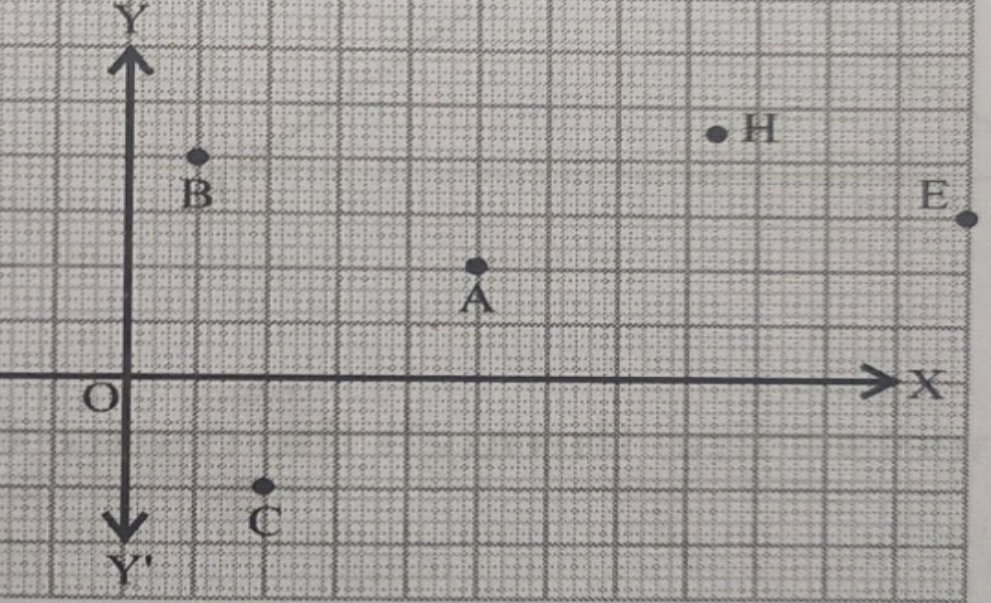
Refer to the points D and C, find the distance between the points C and D, if the coordinates of C is (2,-2) and D is (-2,-3)

Refer to point B and C, If B is consider as origin then what are coordinates of C ?

If point P divides the line segment BC in 1:2. Find coordinates of P.
OR
Find the mid point of line segment AD .