Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

Table of Contents

Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

Class 10 Maths MCQs for Chapter 1 (Real Numbers) are available online here with answers. All these objective questions are prepared as per the latest CBSE syllabus and NCERT guidelines. MCQs for Class 10 Maths Chapter 1 are prepared according to the new exam pattern. Solving these multiple-choice questions will help students to score good marks in the board exams

Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

1. The decimal expansion of 22/7 is

(a) Terminating

(b) Non-terminating and repeating

(d) None of the above

2. For some integer n, the odd integer is represented in the form of:

(a) n

(b) n + 1

(d) 2n

3. HCF of 26 and 91 is:

(a) 15

(b) 13

(d) 11

4. Which of the following is not irrational?

(a) (3 + √7)

(b) (3 – √7)

(d) 3√7

5. The addition of a rational number and an irrational number is equal to:

(a) rational number

(b) Irrational number

(d) None of the above

Answer: (b) Irrational number

The addition of a rational number and an irrational number is equal to irrational number.

6. The multiplication of two irrational numbers is:

(a) irrational number

(b) rational number

(d) None

7. If set A = {1, 2, 3, 4, 5,…} is given, then it represents:

(a) Whole numbers

(b) Rational Numbers

(d) Complex numbers

8. If p and q are integers and is represented in the form of p/q, then it is a:

(a) Whole number

(b) Rational number

(d) Even number

9. The largest number that divides 70 and 125, which leaves the remainders 5 and 8, is:

(a) 65

(b) 15

(d) 25

10. The least number that is divisible by all the numbers from 1 to 5 is:

(a) 70

(b) 60

11. The sum or difference of two irrational numbers is always

(a) rational

(b) irrational

(d) not determined

12. The decimal expansion of the rational number 23/(2² . 5) will terminate after

(a) one decimal place

(b) two decimal places

(d) more than 3 decimal places

13. Euclid’s division lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy

(a) 1 < r < b

(b) 0 < r ≤ b

(d) 0 < r < b

14. For some integer m, every even integer is of the form

(a) m

(b) m + 1

(d) 2m + 1

15. Using Euclid’s division algorithm, the HCF of 231 and 396 is

22. The product of a non-zero rational and an irrational number is
(a) always rational
(b) rational or irrational
(c) always irrational
(d) zero

(a) 32

(b) 21

(d) 33

Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

16. If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is

(a) 4

(b) 2

(d) 3

17. The prime factorisation of 96 is

(a) 2⁵ × 3

(b) 2⁶

(d) 2⁴ × 32

18. For any two positive integers a and b, HCF (a, b) × LCM (a, b) =

(a) 1

(b) (a × b)/2

(d) a × b

19. The decimal form of 129225775 is
(a) terminating
(b) non-termining
(c) non-terminating non-repeating
(d) none of the above

20. HCF of 8, 9, 25 is
(a) 8
(b) 9
(c) 25
(d) 1

21. Which of the following is not irrational?
(a) (2 – √3)2
(b) (√2 + √3)2
(c) (√2 -√3)(√2 + √3)
(d)27√7

22. The product of a rational and irrational number is
(a) rational
(b) irrational
(c) both of above
(d) none of above

23. The sum of a rational and irrational number is
(a) rational
(b) irrational
(c) both of above
(d) none of above

24. The product of two different irrational numbers is always
(a) rational
(b) irrational
(c) both of above
(d) none of above

24. The sum of two irrational numbers is always
(a) irrational
(b) rational
(c) rational or irrational
(d) one

25. If b = 3, then any integer can be expressed as a =
(a) 3q, 3q+ 1, 3q + 2
(b) 3q
(c) none of the above
(d) 3q+ 1

26. The product of three consecutive positive integers is divisible by
(a) 4
(b) 6
(c) no common factor
(d) only 1

27. The set A = {0,1, 2, 3, 4, …} represents the set of
(a) whole numbers
(b) integers

28. Which number is divisible by 11?
(a) 1516
(b) 1452
(c) 1011
(d) 1121

29. LCM of the given number ‘x’ and ‘y’ where y is a multiple of ‘x’ is given by
(a) x
(b) y
(c) xy
(d) xy

30. The largest number that will divide 398,436 and 542 leaving remainders 7,11 and 15 respectively is
(a) 17
(b) 11
(c) 34
(d) 45

31. There are 312, 260 and 156 students in class X, XI and XII respectively. Buses are to be hired to take these students to a picnic. Find the maximum number of students who can sit in a bus if each bus takes equal number of students
(a) 52
(b) 56
(c) 48
(d) 63

32. There is a circular path around a sports field. Priya takes 18 minutes to drive one round of the field. Harish takes 12 minutes. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet ?
(a) 36 minutes
(b) 18 minutes
(c) 6 minutes
(d) They will not meet

33. Express 98 as a product of its primes
(a) 2² × 7
(b) 2² × 7²
(c) 2 × 7²
(d) 2³ × 7

34. Three farmers have 490 kg, 588 kg and 882 kg of wheat respectively. Find the maximum capacity of a bag so that the wheat can be packed in exact number of bags.
(a) 98 kg
(b) 290 kg
(c) 200 kg
(d) 350 kg

35. For some integer p, every even integer is of the form
(a) 2p + 1
(b) 2p
(c) p + 1
(d) p

36. For some integer p, every odd integer is of the form
(a) 2p + 1
(b) 2p
(c) p + 1
(d) p

37. m² – 1 is divisible by 8, if m is
(a) an even integer
(b) an odd integer
(c) a natural number
(d) a whole numberAnswer

38. If two positive integers A and B can be ex-pressed as A = xy3 and B = xiy2z; x, y being prime numbers, the LCM (A, B) is
(a) xy²
(b) x⁴y²z
(c) x⁴y³
(d) x⁴y³

39. The product of a non-zero rational and an irrational number is
(a) always rational
(b) rational or irrational
(c) always irrational
(d) zero

40. If two positive integers A and B can be expressed as A = xy3 and B = x4y2z; x, y being prime numbers then HCF (A, B) is
(a) xy²
(b) x⁴y²z
(c) x⁴y³
(d) x⁴y³z

41. The largest number which divides 60 and 75, leaving remainders 8 and 10 respectively, is
(a) 260
(b) 75
(c) 65
(d) 13

42. The least number that is divisible by all the numbers from 1 to 5 (both inclusive) is
(a) 5
(b) 60
(c) 20
(d) 100

43. The least number that is divisible by all the numbers from 1 to 8 (both inclusive) is
(a) 840
(b) 2520
(c) 8
(d) 420

44. The decimal expansion of the rational number 14587250 will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places

45. The decimal expansion of the rational number 972×54 will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places

46. The product of two consecutive natural numbers is always:
(a) prime number
(b) even number
(c) odd number
(d) even or odd

47. If the HCF of 408 and 1032 is expressible in the form 1032 x 2 + 408 × p, then the value of p is
(a) 5
(b) -5
(c) 4
(d) -4

48. The number in the form of 4p + 3, where p is a whole number, will always be
(a) even
(b) odd
(c) even or odd
(d) multiple of 3

49. When a number is divided by 7, its remainder is always:
(a) greater than 7
(b) at least 7
(c) less than 7
(d) at most 7

50. (6 + 5 √3) – (4 – 3 √3) is
(a) a rational number
(b) an irrational number
(c) a natural number
(d) an integer

51. If HCF (16, y) = 8 and LCM (16, y) = 48, then the value of y is
(a) 24
(b) 16
(c) 8
(d) 48

52. According to the fundamental theorem of arith-metic, if T (a prime number) divides b2, b > 0, then
(a) T divides b
(b) b divides T
(c) T2 divides b2
(d) b2 divides T2

53. The number ‘π’ is
(a) natural number
(b) rational number
(c) irrational number
(d) rational or irrational

54. For any positive integer a and b, there exist unique integers q and r such that a = 3q + r, where r must satisfy.
(a) 0 ≤ r < 3
(b) 1 < r < 3
(c) 0 < r < 3
(d) 0 < r ≤ 3

55. The values of x and y is the given figure are

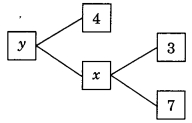
MCQ Questions for Class 10 Maths Chapter 1 Real Numbers with Answers

(a) x + 10, y = 14
(b) x = 21, y = 84
(c) x = 21, y = 25
(d) x = 10, y = 40

56. HCF (a, b) = 12 and a × b = 1800 then LCM (a, b) is
(a) 3600
(b) 900
(c) 150
(d) 90

57. If mⁿ = 32, where m and n are positive integers, then the value of (n)^mn is
(a) 9765625
(b) 9775625
(c) 9785625
(d) 9865625

58.The decimal expansion of 178 will terminate after how many places of decimals?
(a) 1
(b) 2
(c) 3
(d) will not terminate

59. If HCF of 55 and 99 is expressible in the form 55 m – 99, then the value of m:
(a) 4
(b) 2
(c) 1
(d) 3

60. If A = 2n + 13, B = n + 7 where n is a natural number then HCF of A and B
(a) 2
(b) 1
(c) 3
(d) 4

61. (-1)ⁿ + (-1)⁸ⁿ = 0 when n is
(a) any positive integer
(b) any odd natural number
(c) any even numeral number
(d) any negative integer

62. If the LCM of 12 and 42 is 10 m + 4 then the value of m is
(a) 50
(b) 8
(c) 15
(d) l

63. The decimal expansion of the rational number 624322×54 will terminate after
(a) 4 places of decimal
(b) 3 places of decimal
(c) 2 places of decimal
(d) 1 place of decimal

64. n² – 1 is divisible by 8, if n is(a) an integer
(b) a natural number
(c) an odd natural number
(d) an even natural number

65. If n is a natural number, then exactly one of numbers n, n + 2 and n + 1 must be a multiple of
(a) 2
(b) 3
(c) 5
(d) 7

66. The rational number between 72 and 73 is
(a) 65
(b) 34
(c) 32
(d) 45

67. If a and b are two positive numbers and H and L are their HCF and LCM respectively. Then
(a) a × b = H × L
(b) a = b × H
(c) a = b×LH
(d) H = La×b

68. LCM of 2³ × 3² and 2² × 3³ is
(a) 2³
(b) 3³
(c) 2³ × 3³
(d) 2² × 3²

69. The LCM of 2.5, 0.5 and 0.175 is
(a) 2.5
(b) 5
(c) 7.5
(d) 0.875

Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

70.The decimal form of

$\frac{129}{2^{2} 5^{7} 7^{5}}$ is
(a) terminating
(b) non-termining
(c) non-terminating non-repeating
(d) none of the aboveAnswer

71. HCF of 8, 9, 25 is
(a) 8
(b) 9
(c) 25
(d) 1

72. The sum of a rational and irrational number is
(a) rational
(b) irrational
(c) both of above
(d) none of above

73. The product of two different irrational numbers is always
(a) rational
(b) irrational
(c) both of above
(d) none of above

74. The sum of two irrational numbers is always
(a) irrational
(b) rational
(c) rational or irrational
(d) one

75. The product of three consecutive positive integers is divisible by
(a) 4
(b) 6
(c) no common factor
(d) only 1

76. The largest number that will divide 398,436 and 542 leaving remainders 7,11 and 15 respectively is
(a) 17
(b) 11
(c) 34
(d) 45

77. There are 312, 260 and 156 students in class X, XI and XII respectively. Buses are to be hired to take these students to a picnic. Find the maximum number of students who can sit in a bus if each bus takes equal number of students
(a) 52
(b) 56
(c) 48
(d)

78. There is a circular path around a sports field. Priya takes 18 minutes to drive one round of the field. Harish takes 12 minutes. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet ?
(a) 36 minutes
(b) 18 minutes
(c) 6 minutes
(d) They will not meet

79. Express 98 as a product of its primes
(a) 2²x7
(b) 2²x7²
(c) 2×7²
(d) 2³x7

80. Three farmers have 490 kg, 588 kg and 882 kg of wheat respectively. Find the maximum capacity of a bag so that the wheat can be packed in exact number of bags.
(a) 98 kg
(b) 290 kg
(c) 200 kg
(d) 350 kg

81. If two positive integers A and B can be ex-pressed as A = xy3 and B = xy2; x, y being prime numbers, the LCM (A, B) is
(a) xy²
(b) x⁴y²z
(c) x⁴y³
(d) x⁴y³z

82. The least number that is divisible by all the numbers from 1 to 5 (both inclusive) is
(a) 5
(b) 60
(c) 20
(d) 100

83. The product of two consecutive natural numbers is always:
(a) prime number
(b) even number
(c) odd number
(d) even or odd

84. If the HCF of 408 and 1032 is expressible in the form 1032 x 2 + 408xp, then the value of p is
(a) 5
(b) -5
(c) 4
(d) -4

85. The number in the form of 4p + 3, where p is a whole number, will always be
(a) even
(b) odd
(c) even or odd
(d) multiple of 3

86. When a number is divided by 7, its remainder is always:
(a) greater than 7
(b) at least 7
(c) less than 7
(d) at most 7

87. If HCF (16, y) = 8 and LCM (16, y) = 48, then the value of y is
(a) 24
(b) 16
(c) 8
(d) 48

88. If LCM (77, 99) = 693, then HCF (77, 99) is
(a) 11
(b) 7
(c) 9
(d) 22

89. For positive integers a and 3, there exist unique integers q and r such that a = 3q + r, where r must satisfy:
(a) 0 < r < 3
(b) 1 < r < 3
(c) 0 < r < 3
(d) 0 < r < 3

90. Find the greatest number of 5 digits, that will give us remainder of 5 when divided by 8 and 9 respectively.
(a) 99921
(b) 99931
(c) 99941
(d) 99951

91. For some integers p and 5, there exist unique integers q and r such that p =5q + r. Possible values of r are
(a) 0 or 1
(b) 0, 1 or 2
(c) 0, 1, 2 or 3
(d) 0, 1, 2, 3 or 4

92. The ratio between the LCM and HCF of 5, 15, 20 is:
(a) 9 : 1
(b) 4:3
(c) 11:1
(d) 12:1

93. Two alarm clocks ring their alarms at regular intervals of 50 seconds and 48 seconds. If they first beep together at 12 noon, at what time will they beep again for the first time ?
(a) 12.20 pm
(b) 12.12 pm
(c) 12.11pm
(d) none of these

94. There are 576 boys and 448 girls in a school that are to be divided into equal sections of either boys or girls alone. The total number of sections thus formed are:
(a) 22
(b) 16
(c) 36
(d) 21

95. Two natural numbers whose difference is 66 and the least common multiple is 360, are:
(a) 120 and 54
(b) 90 and 24
(c) 180 and 114
(d) 130 and 64

96. The product of three consecutive positive integers is divisible by
(a) 4
(b) 6
(c) no common factor
(d) only 1

97. LCM of the given number ‘x’ and ‘y’ where y is a multiple of ‘x’ is given by
(a) x
(b) y
(c) xy
(d) xy

98. The largest number that will divide 398,436 and 542 leaving remainders 7,11 and 15 respectively is
(a) 17
(b) 11
(c) 34
(d) 45

99. There is a circular path around a sports field. Priya takes 18 minutes to drive one round of the field. Harish takes 12 minutes. Suppose they both start at the same point and at the same time and go in the same direction. After how many minutes will they meet ?
(a) 36 minutes
(b) 18 minutes
(c) 6 minutes
(d) They will not meet

100. Three farmers have 490 kg, 588 kg and 882 kg of wheat respectively. Find the maximum capacity of a bag so that the wheat can be packed in exact number of bags.
(a) 98 kg
(b) 290 kg
(c) 200 kg
(d) 350 kg

MCQ VIDEOS ALL CHAPTERS CLASS 10 MATHShttps://www.youtube.com/watch?v=-eBlHyBxjLg&list=PL2uPMjJCHErQZZNipbsnagBqPrCU_WRN8

Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

Class 10 Maths Chapter 1 Real Numbers MCQs with Answers

MCQ Questions for Class 10 Maths all Chaptershttps://sharmatutorial.in/category/mcq-class-10-maths/

Leave a Comment Cancel Reply